Vous avez probablement au moins une familiarité avec la transformée de Fourier, un processus mathématique pour transformer un signal du domaine temporel en un signal du domaine fréquentiel. En particulier, pour les ordinateurs, nous n’avons pas vraiment une belle équation donc nous utilisons la version discrète de la transformée qui prend une série de mesures à intervalles réguliers. Si vous avez besoin de comprendre tout le spectre de fréquences d’un signal ou si vous voulez filtrer des parties du signal, c’est certainement l’outil pour le travail. Cependant, parfois, c’est plus que ce dont vous avez besoin.
Par exemple, pensez à accorder une corde de guitare. Vous avez seulement besoin de savoir si une fréquence est présente ou si ce n’est pas le cas. Si vous décodez des TouchTones, il vous suffit de savoir si deux des huit fréquences sont présentes. Vous ne vous souciez de rien d’autre.
Une transformée de Fourier peut faire l’un ou l’autre de ces emplois. Mais si vous suivez cette voie, vous allez faire beaucoup de maths pour calculer des choses qui ne vous intéressent pas, juste pour pouvoir choisir le ou les éléments qui vous intéressent. C’est l’idée derrière le Goertzel. Il s’agit essentiellement d’un algorithme de transformation de Fourier rapide dépouillé pour ne calculer qu’une seule bande de fréquences d’intérêt. Le calcul est beaucoup plus facile et vous pouvez généralement l’implémenter plus rapidement et plus petit qu’une transformation complète, même sur de petits processeurs.
Fourier en revue
Juste pour passer en revue, un système typique qui utilise une transformée de Fourier lira un certain nombre d’échantillons à une certaine fréquence d’horloge à l’aide d’un convertisseur analogique-numérique. Par exemple, vous pouvez lire 1024 échantillons à 1 MHz. Chaque échantillon sera 1 microseconde après l’échantillon précédent, et vous obtiendrez un peu plus d’une milliseconde de données.
La transformation produira également 1024 résultats, souvent appelés buckets. Chaque seau représentera 1/1024 du 1 MHz. En raison de la limite de Nyquist, la moitié supérieure des résultats n’est pas très utile, donc de manière réaliste, les 512 premiers seaux représenteront 0 Hz à 500 Hz.
Voici une feuille de calcul (après tout, il s’agit de la série d’articles DSP Spreadsheet) qui utilise le module complémentaire d’analyse XLMiner pour effectuer des transformations de Fourier. La fréquence d’échantillonnage est de 1024 Hz, donc chaque compartiment (colonne G) vaut 1 Hz. La colonne B génère deux ondes sinusoïdales ensemble à 100 Hz et 20 Hz. Nous avons parlé de générer des signaux comme celui-ci l’année dernière.
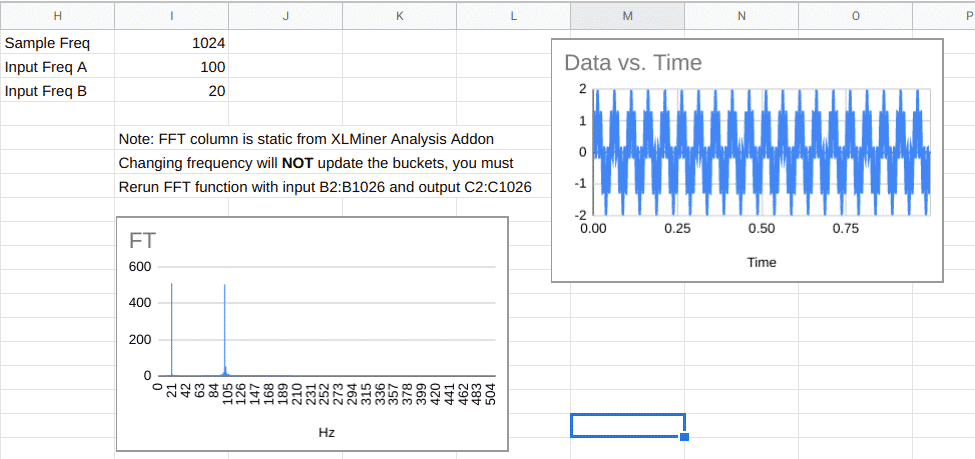
Les données FFT de la colonne C sont des nombres complexes et ne sont pas mises à jour en direct. Vous devez utiliser le module complémentaire XLMiner pour le recalculer si vous changez de fréquence. L’amplitude des nombres apparaît dans la colonne F et vous verrez que les buckets qui correspondent aux deux fréquences d’entrée seront beaucoup plus élevés que les autres buckets.
Un seau de plusieurs
Si notre objectif était de savoir si le signal contenait le signal de 100 Hz, nous pourrions simplement calculer la cellule F102, si nous savions comment. C’est exactement ce que fait le Goertzel. Voici la formule réelle pour chaque compartiment dans une transformation de Fourier discrète (avec l’aimable autorisation de Wikipedia):
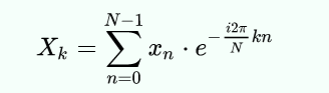
Si vous appliquez la formule d’Euler, vous obtenez:

Mathématiquement, N est la taille du bloc, k est le numéro de compartiment d’intérêt, xn est le nième échantillon. Puisque n varie de 0 à N-1, vous pouvez voir que cette expression utilise toutes les données pour calculer la valeur de chaque compartiment.
L’astuce, alors, est de trouver le nombre minimum d’étapes dont nous avons besoin pour calculer un seul compartiment. Gardez à l’esprit que pour une transformation complète, vous devez faire ce calcul pour chaque compartiment. Ici, nous n’avons besoin de le faire que pour un. Cependant, vous devez tout résumer.
Couper à la chasse
Si vous faites un peu de manipulation, vous pouvez la réduire aux étapes suivantes:
- Précalculez le rapport de fréquence en radians qui est de 2Πk / N
- Calculez le cosinus de la valeur que vous avez trouvée à l’étape 1 (appelez ce C); calculer également le sinus (appelez ce S)
- Pour chaque bucket dans l’ordre, prenez la valeur du bucket précédent (P) et du bucket avant celui (R) et calculez bucket = 2 * C * PR, puis ajoutez la valeur d’entrée actuelle
- Maintenant, le dernier compartiment sera configuré pour vous donner presque la valeur du kième compartiment. Pour trouver la partie réelle, multipliez le bucket final par C et soustrayez P. Pour la partie imaginaire, multipliez S par la valeur finale du bucket
- Vous voulez maintenant trouver la grandeur du nombre complexe formé par les parties réelle et imaginaire. C’est facile à faire si vous convertissez en notation polaire (trouvez l’hypoténuse du triangle formé par la partie réelle et imaginaire).
Bien sûr, il existe également une feuille de calcul pour cela. Avec les limites d’une feuille de calcul, elle effectue beaucoup de calculs supplémentaires, donc pour compenser cela, la colonne D masque toutes les lignes qui n’ont pas d’importance. Dans un programme réel, vous ne feriez tout simplement pas ces calculs (colonnes EG) sauf pour la dernière fois dans la boucle (c’est-à-dire sur chaque ligne). Vous avez besoin de quelques échantillons pour amorcer la pompe, les deux premières lignes sont donc grisées.

Il y a aussi d’autres optimisations que vous feriez. Par exemple, le terme cosinus est doublé à chaque fois dans la boucle mais pas sur le calcul final. Dans un vrai programme, vous feriez ce calcul une fois, mais pour une petite feuille de calcul, il n’y a pas beaucoup de différence.
La colonne B contient les données d’entrée, bien sûr. La colonne C est le total cumulé des compartiments. Les colonnes EG de la dernière ligne représentent les calculs finaux pour obtenir le résultat complexe du compartiment k. Le véritable endroit pour rechercher les résultats aux alentours de L11. Cette partie de la ligne 11 reprend la partie visible des colonnes EG et met également au carré la grandeur puisque nous recherchons la puissance. Il y a aussi un seuil et une cellule qui vous indiquent si la fréquence (à L1) est présente ou non.
Essayez de changer les fréquences générées et vous verrez qu’il détecte bien les fréquences proches de 20 Hz. Vous pouvez ajuster le seuil pour obtenir une réponse plus serrée ou plus large, mais la différence entre 20 Hz et 19 ou 21 Hz est assez marquée.
Code réel
Puisqu’une feuille de calcul ne vous donne pas vraiment une idée de la façon dont vous feriez vraiment cela dans un langage de programmation conventionnel, voici un pseudo-code:
omega_r = cos(2.0*pi*k/N);
omega_r2=2*omega_r;
omega_i = sin(2.0*pi*k/N);
P = 0.0;
S = 0.0;
for (n=0; n<N; ++n)
{
y = x(n) + omega_r2*P -S;
S = P;
P = y;
}
realy = omega_r*P - S; // note that hear P=last result and S is the one before
imagy=omega_i*P;
magy=abs(complex(realy,imagy)); // mag=sqrt(r^2+i^2);
Puisque vous pouvez précalculer tout ce qui se trouve en dehors de la boucle, cela est assez facile à formuler même dans un simple processeur. Vous pouvez même ignorer la racine carrée si vous ne faites que des comparaisons et que vous souhaitez quand même mettre le résultat au carré.
Les compromis
N’oubliez pas, tout est un compromis. La fréquence d’échantillonnage et le nombre d’échantillons déterminent le temps nécessaire à la lecture de chaque échantillon et également la largeur de la plage de fréquences du compartiment. Si vous devez sonder de nombreuses fréquences, vous pourriez être mieux avec une bibliothèque de transformées de Fourier bien implémentée.
Il existe d’autres moyens d’optimiser les deux algorithmes. Par exemple, vous pouvez limiter la quantité de données que vous traitez en sélectionnant la fréquence d’échantillonnage et la taille de bloc appropriées. Ou, au lieu d’utiliser une transformée de Fourier, considérez une transformée de Hartley qui n’utilise pas de nombres complexes.
En pratique
Je doute très sérieusement que quiconque ait besoin de faire ce genre de logique dans une feuille de calcul. Mais comme les autres modèles de feuilles de calcul DSP, il est très facile d’examiner et d’expérimenter l’algorithme ainsi présenté. Développer l’intuition sur les algorithmes est au moins aussi important que leur souvenir par cœur – peut-être est-ce encore plus important.
Le Goertzel est un moyen facile d’éviter un algorithme plus compliqué pour de nombreux cas courants. C’est un outil que vous devriez avoir dans votre boîte de trucs.