À moins que vous ne soyez physicien ou ingénieur, il n’y a vraiment pas beaucoup de raisons pour vous de connaître les équations aux dérivées partielles. Je sais. Après des années à les étudier au premier cycle pendant mes études de génie mécanique, je ne les ai jamais utilisées depuis dans le monde réel.
Mais les équations aux dérivées partielles, ou PDE, sont également un peu magiques. Il s’agit d’une catégorie d’équations mathématiques qui décrivent très bien les changements dans l’espace et le temps, et donc très pratiques pour décrire les phénomènes physiques dans notre univers. Ils peuvent être utilisés pour tout modéliser, des orbites planétaires à la tectonique des plaques en passant par la turbulence de l’air qui perturbe un vol, ce qui nous permet à son tour de faire des choses pratiques comme prédire l’activité sismique et concevoir des avions sûrs.
Le problème est que les PDE sont notoirement difficiles à résoudre. Et ici, la signification de «résoudre» est peut-être mieux illustrée par un exemple. Supposons que vous essayez de simuler la turbulence de l’air pour tester une nouvelle conception d’avion. Il existe un PDE connu appelé Navier-Stokes qui est utilisé pour décrire le mouvement de tout fluide. «Résoudre» Navier-Stokes vous permet de prendre un instantané du mouvement de l’air (alias les conditions de vent) à tout moment et de modéliser comment il continuera à se déplacer ou comment il se déplaçait auparavant.
Ces calculs sont très complexes et intensifs en calcul, c’est pourquoi les disciplines qui utilisent beaucoup d’EDP s’appuient souvent sur des supercalculateurs pour faire le calcul. C’est aussi pourquoi le domaine de l’IA s’est particulièrement intéressé à ces équations. Si nous pouvions utiliser l’apprentissage en profondeur pour accélérer le processus de résolution de ces problèmes, cela pourrait faire beaucoup de bien pour la recherche scientifique et l’ingénierie.
Maintenant, les chercheurs de Caltech ont introduit une nouvelle technique d’apprentissage en profondeur pour résoudre les PDE qui est considérablement plus précise que les méthodes d’apprentissage en profondeur développées précédemment. Il est également beaucoup plus généralisable, capable de résoudre des familles entières de PDE – comme l’équation de Navier-Stokes pour tout type de fluide – sans nécessiter de recyclage. Enfin, il est 1 000 fois plus rapide que les formules mathématiques traditionnelles, ce qui faciliterait notre dépendance aux supercalculateurs et augmenterait notre capacité de calcul à modéliser des problèmes encore plus importants. C’est vrai. L’amener sur.
Temps de marteau
Avant de nous plonger dans la façon dont les chercheurs ont fait cela, apprécions d’abord les résultats. Dans le gif ci-dessous, vous pouvez voir une démonstration impressionnante. La première colonne montre deux instantanés du mouvement d’un fluide; la seconde montre comment le fluide a continué à se déplacer dans la vie réelle; et le troisième montre comment le réseau neuronal a prédit que le fluide se déplacerait. Il semble fondamentalement identique au second.
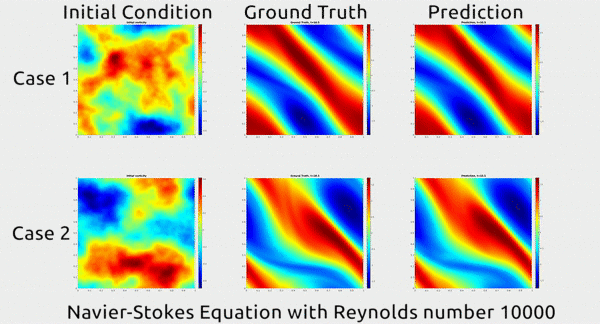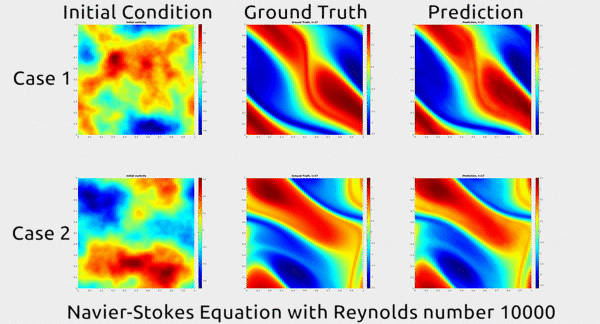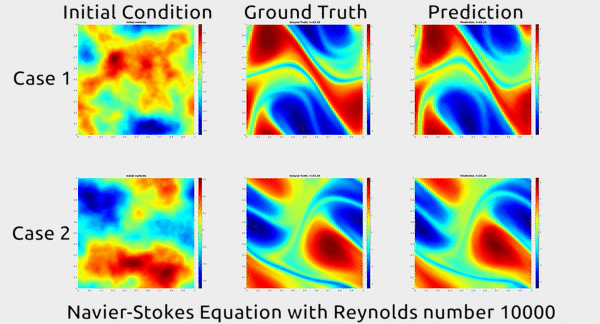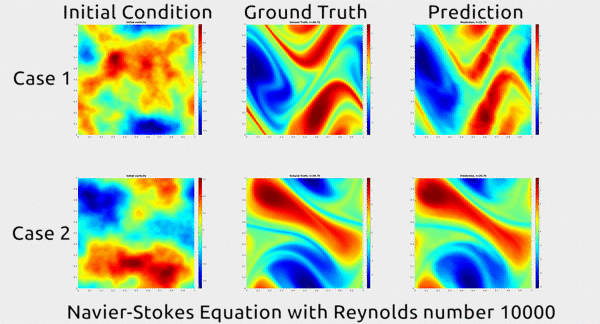
Selon dentpourdent.net, le papier a obtenu beaucoup de buzz sur Twitter, et même un cri du rappeur MC Hammer. Oui vraiment.
Bon, revenons à comment ils l’ont fait.
Quand la fonction s’adapte
La première chose à comprendre ici est que les réseaux de neurones sont fondamentalement des approximateurs de fonctions. (Dites quoi?) Lorsqu’ils s’entraînent sur un ensemble de données d’entrées et de sorties appariées, ils calculent en fait la fonction, ou une série d’opérations mathématiques, qui se transposeront l’une dans l’autre. Pensez à construire un détecteur de chat. Vous entraînez le réseau de neurones en le nourrissant de nombreuses images de chats et d’objets qui ne sont pas des chats (les entrées) et en étiquetant chaque groupe avec un 1 ou 0, respectivement (les sorties). Le réseau de neurones recherche alors la meilleure fonction qui peut convertir chaque image d’un chat en 1 et chaque image de tout le reste en 0. C’est ainsi qu’il peut regarder une nouvelle image et vous dire si c’est un chat ou non. Il utilise la fonction qu’il a trouvée pour calculer sa réponse – et si son entraînement a été bon, il y parviendra la plupart du temps.
De manière pratique, ce processus d’approximation de fonction est ce dont nous avons besoin pour résoudre une PDE. Nous essayons finalement de trouver une fonction qui décrit le mieux, par exemple, le mouvement des particules d’air dans l’espace physique et le temps.
Voici maintenant le nœud du papier. Les réseaux de neurones sont généralement formés pour approximer les fonctions entre les entrées et les sorties définies dans l’espace euclidien, votre graphe classique avec les axes x, y et z. Mais cette fois, les chercheurs ont décidé de définir les entrées et les sorties dans l’espace de Fourier, qui est un type spécial de graphique pour tracer les fréquences d’onde. Selon Anima Anandkumar, professeur à Caltech qui a supervisé la recherche, ils se sont inspirés de leur travail dans d’autres domaines, c’est que quelque chose comme le mouvement de l’air peut en fait être décrit comme une combinaison de fréquences d’ondes. La direction générale du vent au niveau macro est comme une basse fréquence avec de très longues ondes léthargiques, tandis que les petits tourbillons qui se forment au niveau micro sont comme des fréquences élevées avec des ondes très courtes et rapides.
Pourquoi est-ce important? Parce qu’il est beaucoup plus facile d’approcher une fonction de Fourier dans l’espace de Fourier que de se débattre avec des PDE dans l’espace euclidien, ce qui simplifie grandement le travail du réseau neuronal. Cue des gains de précision et d’efficacité majeurs: en plus de son énorme avantage en termes de vitesse par rapport aux méthodes traditionnelles, leur technique atteint un taux d’erreur 30% inférieur lors de la résolution de Navier-Stokes par rapport aux méthodes d’apprentissage en profondeur précédentes.
Le tout est extrêmement intelligent et rend également la méthode plus généralisable. Les anciennes méthodes d’apprentissage en profondeur devaient être entraînées séparément pour chaque type de fluide, alors que celui-ci n’a besoin d’être formé qu’une seule fois pour les gérer tous, comme l’ont confirmé les expériences des chercheurs. Bien qu’ils n’aient pas encore essayé d’étendre cela à d’autres exemples, il devrait également être capable de gérer toutes les compositions de la terre lors de la résolution des PDE liés à l’activité sismique, ou de chaque type de matériau lors de la résolution des PDE liés à la conductivité thermique.
Super-simulation
Anandkumar et l’auteur principal de l’article, Zongyi Li, étudiante en doctorat dans son laboratoire, n’ont pas fait cette recherche uniquement pour le plaisir théorique. Ils veulent amener l’IA à plus de disciplines scientifiques. C’est en discutant avec divers collaborateurs en science du climat, en sismologie et en science des matériaux qu’Anandkumar a décidé pour la première fois de relever le défi du PDE avec ses étudiants. Ils travaillent maintenant à mettre leur méthode en pratique avec d’autres chercheurs de Caltech et du Lawrence Berkeley National Laboratory.
Un sujet de recherche qui intéresse particulièrement Anandkumar: le changement climatique. Navier-Stokes n’est pas seulement doué pour modéliser la turbulence de l’air; il est également utilisé pour modéliser les conditions météorologiques. «Avoir de bonnes prévisions météorologiques précises à l’échelle mondiale est un problème tellement difficile», dit-elle, «et même sur les plus gros superordinateurs, nous ne pouvons pas le faire à l’échelle mondiale aujourd’hui. Donc, si nous pouvons utiliser ces méthodes pour accélérer l’ensemble du pipeline, cela aura un impact énorme. »
Il y a aussi beaucoup, beaucoup plus d’applications, ajoute-t-elle. «En ce sens, le ciel est la limite, car nous avons un moyen général d’accélérer toutes ces applications.»