Comment fonctionnent les bits
Vous avez probablement déjà entendu dire que les ordinateurs stockent des objets dans 1le sable 0s. Ces unités d’information fondamentales sont appelées morceaux. Quand un bit est «allumé», cela correspond à un 1; quand il est «éteint», il se transforme en 0. Chaque bit, en d’autres termes, ne peut stocker que deux informations.
Mais une fois que vous les associez, la quantité d’informations que vous pouvez encoder augmente de manière exponentielle. Deux bits peuvent représenter quatre informations car il existe 2 ^ 2 combinaisons: 00, 01, dix, et 11. Quatre bits peuvent représenter 2 ^ 4 ou 16 éléments d’information. Huit bits peuvent représenter 2 ^ 8 ou 256. Et ainsi de suite.
La bonne combinaison de bits peut représenter des types de données comme des nombres, des lettres et des couleurs, ou des types d’opérations comme l’addition, la soustraction et la comparaison. La plupart des ordinateurs portables de nos jours sont des ordinateurs 32 ou 64 bits. Cela ne veut pas dire que l’ordinateur ne peut encoder que 2 ^ 32 ou 2 ^ 64 éléments d’information au total. (Ce serait un ordinateur très faible.) Cela signifie qu’il peut utiliser autant de bits de complexité pour coder chaque élément de données ou opération individuelle.
Apprentissage en profondeur 4 bits
Alors, que signifie la formation 4 bits? Eh bien, pour commencer, nous avons un ordinateur 4 bits, et donc 4 bits de complexité. Une façon de penser à cela: chaque nombre que nous utilisons pendant le processus de formation doit être l’un des 16 nombres entiers compris entre -8 et 7, car ce sont les seuls nombres que notre ordinateur peut représenter. Cela vaut pour les points de données que nous alimentons dans le réseau de neurones, les nombres que nous utilisons pour représenter le réseau de neurones et les nombres intermédiaires que nous devons stocker pendant l’entraînement.
Alors, comment faisons-nous cela? Pensons d’abord aux données d’entraînement. Imaginez que ce soit tout un tas d’images en noir et blanc. Première étape: nous devons convertir ces images en nombres pour que l’ordinateur puisse les comprendre. Pour ce faire, nous représentons chaque pixel en fonction de sa valeur de niveaux de gris: 0 pour le noir, 1 pour le blanc et les décimales entre les nuances de gris. Notre image est maintenant une liste de nombres allant de 0 à 1. Mais dans un pays de 4 bits, nous avons besoin qu’elle varie de -8 à 7. L’astuce ici est de mettre à l’échelle linéairement notre liste de nombres, donc 0 devient -8 et 1 devient 7, et les décimales correspondent aux nombres entiers du milieu. Donc:

Ce processus n’est pas parfait. Si vous avez commencé avec le nombre 0,3, par exemple, vous vous retrouverez avec le nombre mis à l’échelle -3,5. Mais nos quatre bits ne peuvent représenter que des nombres entiers, vous devez donc arrondir -3,5 à -4. Vous finissez par perdre certaines des nuances de gris, ou soi-disant précision, à votre image. Vous pouvez voir à quoi cela ressemble dans l’image ci-dessous.

Cette astuce n’est pas trop minable pour les données d’entraînement. Mais lorsque nous l’appliquons à nouveau au réseau neuronal lui-même, les choses se compliquent un peu.
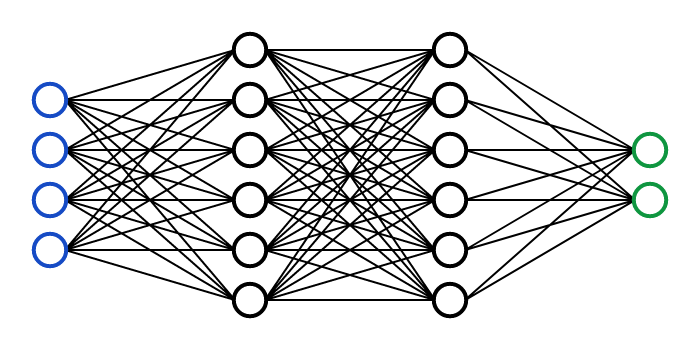
Nous voyons souvent les réseaux de neurones dessinés comme quelque chose avec des nœuds et des connexions, comme l’image ci-dessus. Mais pour un ordinateur, ceux-ci se transforment également en une série de chiffres. Chaque nœud a un soi-disant Activation valeur, qui varie généralement de 0 à 1, et chaque connexion a un poids, qui varie généralement de -1 à 1.
Nous pourrions les mettre à l’échelle de la même manière que nous l’avons fait avec nos pixels, mais les activations et les poids changent également à chaque cycle d’entraînement. Par exemple, les activations varient parfois de 0,2 à 0,9 dans un tour et de 0,1 à 0,7 dans un autre. Le groupe IBM a donc découvert une nouvelle astuce en 2018: redimensionner ces plages pour les étirer entre -8 et 7 à chaque tour (comme indiqué ci-dessous), ce qui évite effectivement de perdre trop de précision.

Mais ensuite, il nous reste un dernier élément: comment représenter en quatre bits les valeurs intermédiaires qui surgissent pendant l’entraînement. Ce qui est difficile, c’est que ces valeurs peuvent s’étendre sur plusieurs ordres de grandeur, contrairement aux nombres que nous traitions pour nos images, pondérations et activations. Ils peuvent être minuscules, comme 0,001, ou énormes, comme 1000. Essayer de mettre à l’échelle de manière linéaire entre -8 et 7 perd toute la granularité à la toute petite extrémité de l’échelle.

Après deux ans de recherche, les chercheurs ont enfin résolu le casse-tête: en empruntant une idée existante à d’autres, ils mettent à l’échelle ces nombres intermédiaires logarithmiquement. Pour voir ce que je veux dire, voici une échelle logarithmique que vous pourriez reconnaître, avec une soi-disant «base» de 10, en utilisant seulement quatre bits de complexité. (Les chercheurs utilisent plutôt une base de 4, car les essais et erreurs ont montré que cela fonctionnait le mieux.) Vous pouvez voir comment cela vous permet d’encoder des nombres petits et grands dans les contraintes de bits.

Avec toutes ces pièces en place, ce dernier article montre comment elles se combinent. Les chercheurs d’IBM ont mené plusieurs expériences dans lesquelles ils simulent une formation 4 bits pour une variété de modèles d’apprentissage profond en vision par ordinateur, en parole et en traitement du langage naturel. Les résultats montrent une perte de précision limitée des performances globales des modèles par rapport à l’apprentissage en profondeur 16 bits. Le processus est également plus de sept fois plus rapide et sept fois plus économe en énergie.