Nous sommes toujours impressionnés par quelque chose de si simple qui peut en fait être si complexe. Par exemple, que penseriez-vous qu’il y ait dans un ordinateur analogique ? Bien sûr, un « vrai » ordinateur analogique a des amplificateurs opérationnels qui peuvent faire des logarithmes, des racines carrées, multiplier et diviser. Mais seriez-vous surpris que vous puissiez créer un appareil analogique comme une règle à calcul en utilisant un pont de Wheatstone – essentiellement deux diviseurs de tension. Vous n’avez même pas besoin d’appareils actifs du tout. C’est une vieille idée qui revenait de temps en temps dans les magazines électroniques. Je vais vous montrer comment ils fonctionnent et simuler l’appareil afin que vous n’ayez pas à le construire, sauf si vous le souhaitez.
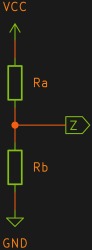Un diviseur de tension est l’un des circuits les plus faciles à analyser au monde. Considérons deux résistances Ra et Rb en série. La tension arrive au sommet de Ra et le bas de Rb est mis à la terre. Le nœud reliant Ra et Rb – appelons-le Z – est ce que nous considérerons comme la sortie.
Disons que nous avons une batterie de 10 V alimentant A et un voltmètre parfait qui ne charge pas le circuit connecté à Z. Par la loi actuelle de Kirchoff, nous savons que le courant à travers Ra et Rb doit être le même. Après tout, il n’y a nulle part où aller. Nous savons également que la chute de tension aux bornes de Ra plus la chute de tension aux bornes de Rb doit être égale à 10 V. Kirchoff, conservation de l’énergie, appelez-la comme vous voulez. Appelons ces quantités I, Va et Vb.
Il y a plusieurs façons de procéder à partir de là, mais acceptons que le courant traversant deux résistances en série soit le même que s’il s’agissait d’une résistance de valeur égale. Autrement dit, une résistance de 1 KΩ et une résistance de 2 KΩ en série tireront autant de courant qu’une résistance de 3 KΩ. Cela signifie que la loi d’Ohm nous dit :
I = 10/(Ra+Rb)
Vous pouvez maintenant résoudre pour chaque chute de tension :
Va = I Ra Vb = I Rb
En fait, notre voltmètre en Z mesurera Vb puisqu’il est à la masse.
Grosse affaire poilue
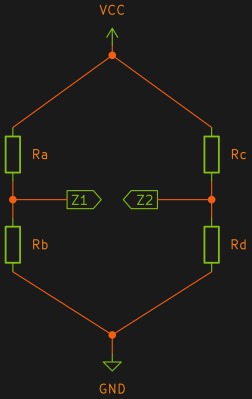Bien sûr, vous connaissez probablement les diviseurs de tension. Mais nous allions parler des ponts de Wheatstone. La vérité est qu’il ne s’agit que de deux diviseurs de tension en parallèle et que vous mesurez la tension entre les deux sorties (appelez-les Z1 et Z2). Vous voyez souvent ce circuit dessiné comme un diamant, mais ne vous y trompez pas. Il ne s’agit toujours que de deux diviseurs de tension.
Sans utiliser de calculs, vous pouvez voir que si les diviseurs de tension sont les mêmes, alors Z1 et Z2 seront les mêmes et, par conséquent, aucun courant ne circulera car la tension entre les deux points est nulle. Que se passe-t-il lorsque le diviseur n’est pas le même ? Il y aura plus de tension sur un point Z que sur l’autre.
Historiquement, cela a été utilisé pour mesurer la résistance. Vous pouvez utiliser deux résistances appariées dans une partie du pont, avoir une résistance inconnue dans l’une des jambes restantes et une résistance variable avec un cadran calibré pour lire les ohms. Vous tournez le cadran jusqu’à ce qu’un mètre indique zéro et lisez la valeur de résistance sur le cadran. Si la source d’alimentation est en courant alternatif, vous pouvez également mesurer la réactance à l’aide d’un circuit similaire.
Mais la règle à calcul ?
Alors, comment passer d’un équipement de test ancien à une règle à calcul ? Changeons le pont pour que le diviseur de gauche ait les résistances Ra et Rb tandis que l’autre a Rc et Rd. On peut regarder l’algèbre :
Z1=V (Rb/(Ra + Rb)) Z2=V (Rd/(Rc + Rd))
On veut que Z1 soit égal à Z2 donc :
V (Rb/(Ra + Rb)) = V (Rd/(Rc + Rd))
Nous pouvons diviser les deux côtés par V et nous débarrasser de ce terme :
(Rb/(Ra + Rb)) = (Rd/(Rc + Rd))
Donc, pour équilibrer le pont, nous avons besoin de :
(Ra + Rb)/Rb = (Rc + Rd)/Rd reciprocal both sides (Ra Rd + Rb Rd) = (Rc Rb + Rb Rd) multiply both sides by Rb Rd Ra Rd = Rc Rb subtract Rb Rd from both sides Ra = (Rb Rc)/Rd Solve for Ra
Comme expérience de pensée simple, imaginez alors que Rd = 1. Si vous définissez Rb et Rc, vous pouvez ajuster Ra pour équilibrer et la valeur de Ra sera la réponse. Ou vous pouvez définir Rb sur 1 et entrer des nombres dans Rc et Rd. Une fois que vous aurez équilibré Ra, vous connaîtrez le résultat de la division.
En pratique, cependant, vous voudrez peut-être mettre à l’échelle le résultat, en particulier pour la division. Par exemple, si Rb = 1, Rc = 2 et Rd = 1000, vous devrez régler A sur 0,002 ohms, ce qui est difficile à faire. Dans ce cas, cependant, vous pouvez définir Rb sur un facteur d’échelle. Si c’était, disons, 10K, alors Ra peut être réglé sur 20 ohms.
Simulation
Vous pouvez casser quelques potentiomètres et essayer cela. Nous suggérons des modèles linéaires à moins que vous ne soyez très habile pour créer des cadrans à échelle logarithmique. Mais comme il s’agit de Circuit VR, nous préférons faire une simulation. Falstad fait l’affaire, mais n’importe quel simulateur est à la hauteur de la tâche.
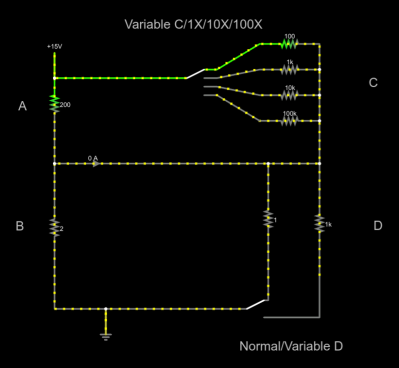
Il y a deux commutateurs dans la simulation. Le commutateur « C » supérieur vous permet de commuter la résistance supérieure ou une résistance de gamme 10X, 100X ou 1000X pour C. Le commutateur « D » inférieur vous permet de sélectionner une résistance de 1 ohm ou une résistance variable pour D. L’ampèremètre dans le le centre montre l’équilibre du pont et lira 0A lorsque vous êtes en équilibre.
En parlant de résistances variables, j’ai mis des curseurs pour chacune des résistances sur la barre latérale droite du simulateur. Cependant, leur utilisation met souvent des valeurs comme 10.002K qui lit 10K à l’écran et est une source d’erreur. Bien sûr, vous auriez le même problème avec de vrais pots, alors c’est peut-être une bonne simulation. Cependant, il est préférable de double-cliquer sur la résistance que vous souhaitez modifier et d’entrer directement sa valeur. Évidemment, vous ne devriez pas changer les trois résistances C fixes ou la résistance D fixe.
Prochaines étapes
Si vous voulez voir à quoi ressemblait ce circuit dans la chair, consultez les pages 48 et 49 de la Radio Electronics de juin 1960. C’est peut-être même l’article même qui a engendré [Bil Herd’s] premier kit informatique. Un kit similaire d’Edmund Scientific utilisait trois potentiomètres pour former le pont dans une configuration commune. Nous avons même vu une version de GE qui utilisait un oscillateur audio pour que vous puissiez entendre le point zéro à l’aide d’un casque. Vous pouvez voir les deux dans l’article commençant à la page 65 du Popular Electronics de décembre 1961. Ou consultez une version plus récente sur Hackaday.io.
Ce serait un projet de jour de pluie assez facile. Si vous avez un compteur à échelle de miroir à l’ancienne d’un ancien multimètre, il brillera vraiment dans cette application. Faire les cadrans dans un programme de CAO et les imprimer serait également sans effort.
Si vous voulez relever un défi, pourquoi ne pas utiliser une source CA avec des condensateurs et des inductances variables pour créer un calculateur de nombres complexes ? Ce serait quelque chose et si vous réussissez, nous le couvririons.
En attendant, nous aimerions souligner que les vrais ordinateurs analogiques n’étaient pas aussi simples. Par contre, par définition, c’est un ordinateur analogique au même titre qu’une vraie règle à calcul. Si vous lisez l’article de Radio Electronics, vous verrez qu’il peut même enchaîner une réponse au problème suivant, comme vous le feriez sur un slipstick.
